|
ESOTERISMO Y SIMBOLO |
|
|
|
|
|
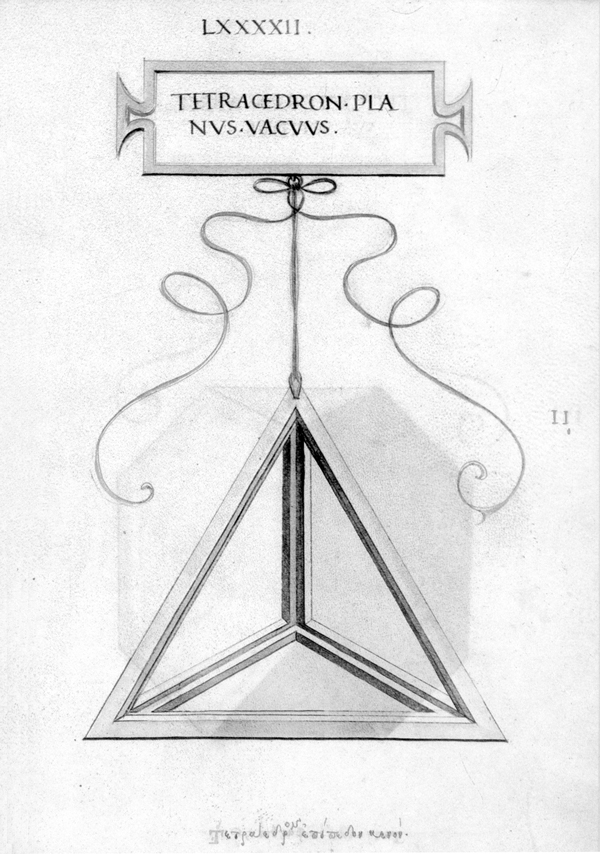
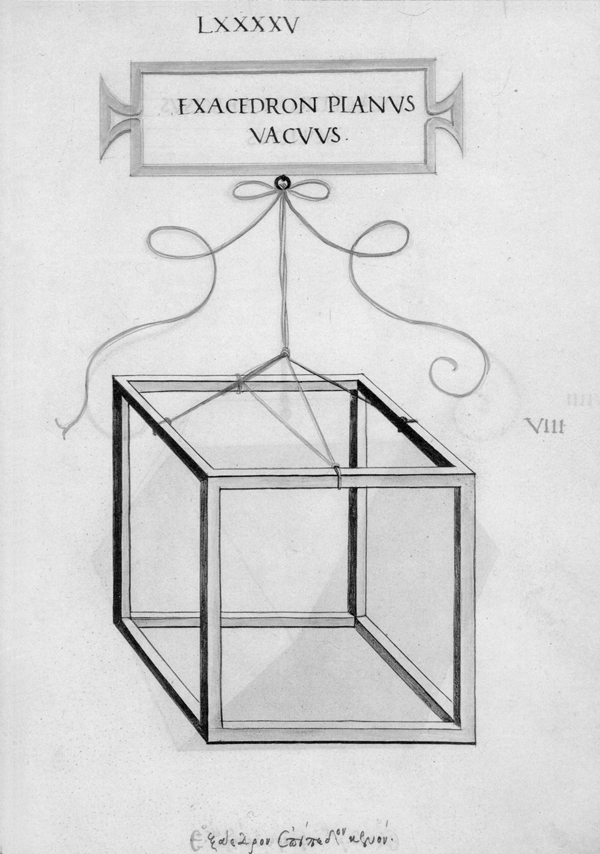
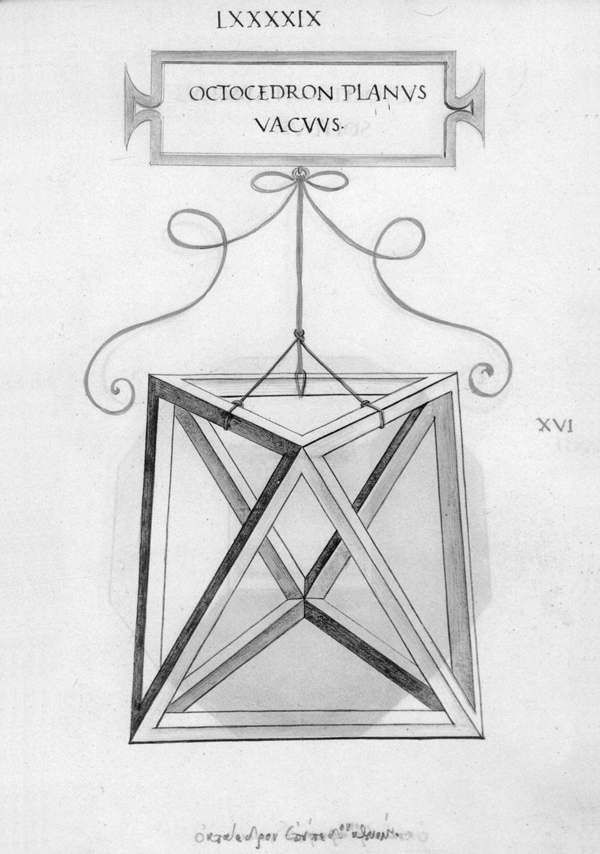
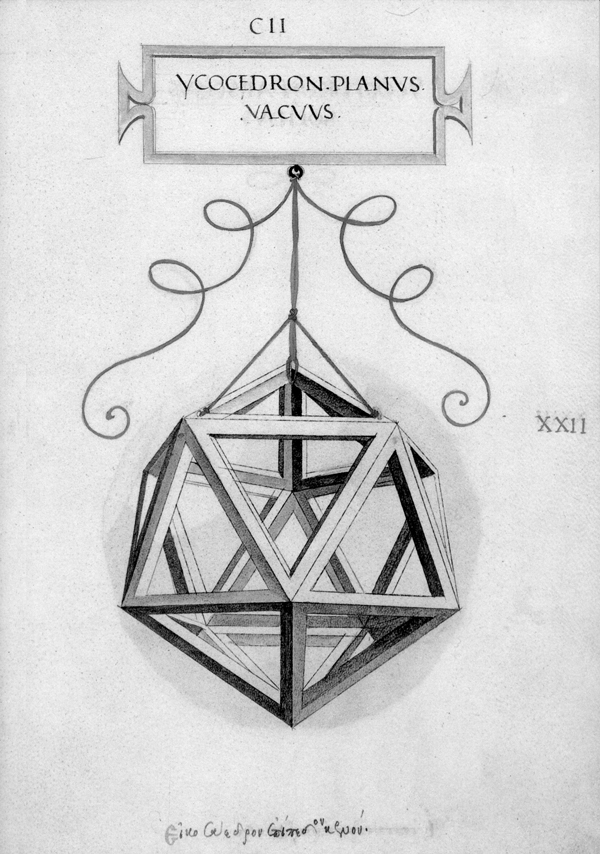
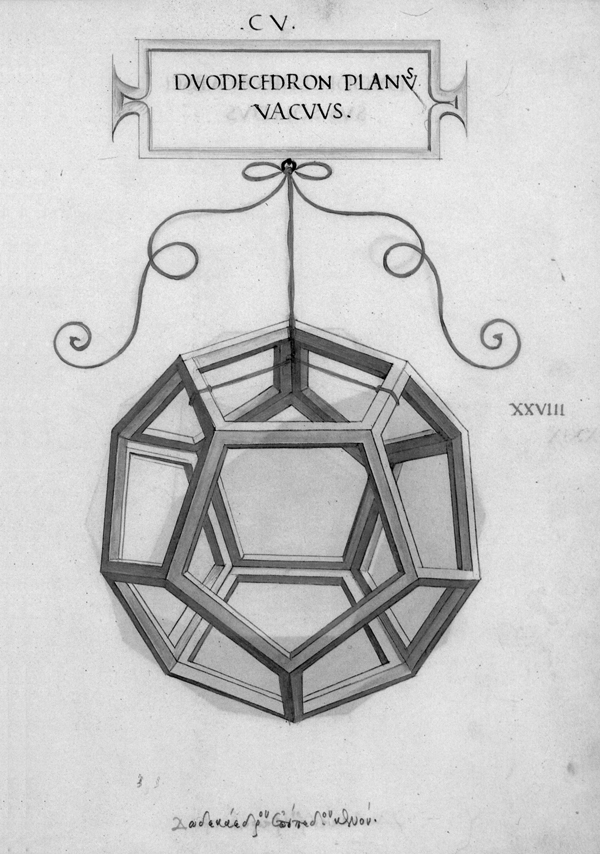
Luca Pacioli. Las matemáticas como utopía … a fines del siglo XV, Italia, con Paolo Toscanelli, Luca Pacioli y Leonardo da Vinci, figuraba sin parangón posible, en matemáticas y en ciencias naturales, a la cabeza de todos los pueblos de Europa, y los sabios de todos los países lo reconocían así y se declaraban sus discípulos, incluso Regiomontanus y Copérnico. A Toscanelli hemos tenido la oportunidad de conocerlo a través de la importancia que Colón le otorgaba como científico; de Leonardo hemos hablado poco y nada aunque su figura incomparable ha sido ya estudiada desde hace años desde el punto de vista tanto esotérico2 como científico, en el sentido de la matemática, la mecánica y las invenciones (últimamente hemos visto exposiciones de sus maquetas e ingenios en varios museos y entidades culturales), etc.; ahora nos toca considerar a Luca Pacioli (1445-1517) y su Divina Proporción. Nos gustaría para introducirnos en su pensamiento ubicarlo en el contexto social y cultural en que le tocó vivir y donde finalmente presenta su obra a su alteza el Duque de Milán en un discurso en el que cita a Nicolás de Cusa, al propio Leonardo, al que se refiere como su compatriota florentino, a Vitruvio, etc. En su Summa de Arithmetica, publicada en Venecia en 1494, –obra anterior a la que estamos considerando y en la que esboza por primera vez a la "divina" proporción– aparecen destacados Platón, Euclides y Boecio, perfilando así lo que será la guía de su tratado, que se basa también en un antecedente medieval, Leonardo de Pisa –como es el caso en relación con Dante y Petrarca en otras disciplinas–, más conocido como Fibonacci (1175-1240), que publicara entre otros el Liber Quadratorum.3 Luca Pacioli nace en el Burgo de Santo Sepulcro, que pertenecía a Florencia, el año 1445. Desde muy joven se lo ve trabajando en pintura y sobre todo en matemática. Pero a los 20 años ya da clases en Venecia De 1475 a 1477 enseña matemáticas en Perugia mientras que cinco años después escribe un tratado de álgebra en Dalmacia. Obtuvo su título de Magister alrededor de 1486-87, y del 1490 a 1493 se radica en su pueblo preparando la edición de la Summa de Arithmetica, Geometria, Proportione et Proportionalità; en ese último año da lecciones públicas de aritmética y geometría en Padua. Ya estamos viendo que nuestro personaje se mueve de corte en corte y de república en república por distintos motivos. Esta constante –que toca a la mayor parte de los hermetistas, alquimistas de la época y filósofos– se hace carne especialmente en Luca Pacioli que viajará por toda Italia hasta su muerte, y lo hará vincularse con una parte importante de los más conocidos esoteristas del momento, que eran acogidos por los distintos príncipes, duques y autoridades de las diferentes ciudades, las cuales competían entre sí por la cultura y refinamiento de sus estados. En 1494 viaja a Venecia para la edición de su Summa. Ese mismo año se dirige a Urbino, a donde su protector Guidobaldo de Montefeltro, hijo y sucesor de su amigo el duque Federico II le invita. El ducado de Urbino será un hogar para el franciscano donde tratará con otros matemáticos y astrónomos, entre ellos Paolo de Mid deburgo a quien él considera el representante más importante de las matemáticas astronómicas. Llamado por el duque de Milán Ludovico Sforza el Moro a enseñar matemáticas en su ciudad, se encuentra allí con Leonardo del que se hace igualmente muy amigo; de esas conversaciones –que versarían también de seguro sobre la colosal estatua ecuestre en bronce que da Vinci había realizado para el duque– se dice que Pacioli se inspiró para darle la forma final a su Divina Proporción que como dijimos ya había bocetado en su Summa.4 Luego de tres años abandona Milán acompañado de Leonardo por la caída política de Ludovico, viajando a Mantua (en donde recibió la hospitalidad de los duques Francisco de Gonzaga e Isabella d’Este, a quienes posteriormente dedicará una obra, De ludis in genere), y Florencia. De ese modo continúa, de corte en corte, su peregrinar, como la mayoría de los sabios de la época que tienen así la fortuna de conocerse personalmente e intercambiar distintos puntos de vista en las diferentes disciplinas tejiendo así la utopía del Renacimiento.5 Entre 1500 y 1505 se lo encuentra en Pisa, Perugia, Bolonia, para finalmente arribar a Florencia donde estrecha lazos con Pietro Soderini, nombrado Magistrado supremo de la república de por vida, que será su protector y a quien hace destinatario moral de la Divina Proporción en su testamento; este Pietro es hermano de Francesco Tomasso Soderini, que defenderá a Ficino con otros cardenales de la acusación de herejía formulada contra él por la publicación de su De Vita coelitus comparanda. De 1505 al 8 se halla en Roma viviendo en la casa y corte del vicecanciller Galeotto Franciotti. Y debe haber sido visto con buenos ojos por el papa Julio II, el cual le concede una curiosa bula que le permite la posesión de bienes materiales. Pasa a Venecia para preparar la edición de los Elementos de Euclides y se retira por cuatro años a su pueblo natal. En 1514 viaja de nuevo a Roma para ocupar la cátedra de matemáticas de la universidad de la Sapienza, a requerimiento del papa León X. Vuelve a su pueblo enfermo en 1517 y allí muere. Es interesante observar que a lo largo de su vida sólo se imprimieron dos de sus tratados, que son la Summa y la Divina Proporción,6 las dos únicas que han llegado a nosotros. La crítica ha indicado que las fuentes, o el legado recibido por Pacioli, se deben fundamentalmente al Timeo de Platón –como él mismo lo dice, y donde se encuentra expresada la «división de un segmento en media y extrema razón»–, los Elementos de Euclides (en cuya proposición VI-XXX se encuentra su formulación, que él en su texto repite), los cuales tradujo y publicó en Venecia en 1509; también la Arquitectura de Vitruvio y la influencia del neoplatonismode la Academia florentina, y desde luego el propio Pitágoras. Su Divina Proporción es una utopía que se da a conocer mediante la expresión matemática, y por lo tanto una de las más claras en su exposición de la visión esotérica-hermética en la que el hombre como microcosmos está integrado en la creación y constituye todo un orden armónico, de arquitectura matemática (y musical). De esta manera es como a Pacioli se le revelan las formas cosmogónicas, puesto que el interés que había desarrollado por este modo del intelecto le había hecho, por ello, el matemático más destacado de su tiempo, y teniendo en cuenta que en su discurso al duque presenta a la divina proporción poco menos que como magia, lo cual involucra a toda la matemática y a todas las proporciones ya que esta ciencia enseñada en sus libros se transforma en teúrgia como debía suceder en vivo y directo desde la época en que la entregara al Moro. En verdad su libro puede verse también como un tratado de matemática, y de hecho de arquitectura. En la voz de su autor: Como se ha dicho, las ciencias y disciplinas matemáticas se encuentran en el primer grado de la certeza y las siguen todas las ciencias naturales; y sin el conocimiento de aquéllas se hace imposible entender bien ninguna otra ciencia. Igualmente está escrito en la sabiduría que omnia consistunt in numero, pondere et mensura, es decir, que todo aquello que se encuentra distribuido por el universo inferior y superior se reduce necesariamente a número, peso y medida. En el capítulo V, donde verdaderamente comienza a referirse al tema del título del libro que estamos comentando, se hace una síntesis feliz de lo expuesto en toda la obra, que fue como ya hemos dicho ilustrada por el propio Leonardo da Vinci con extraordinarios dibujos (donde utilizaba también la perspectiva) acompañando a sus textos: …el título conveniente a nuestro tratado ha de ser el de La Divina Proporción, y ello por numerosas correspondencias de semejanza que encuentro en nuestra proporción, de la que tratamos en este nuestro utilísimo discurso, que corresponden a Dios mismo. Para nuestro propósito será suficiente considerar cuatro de ellas, entre otras. La primera es que ella es una sola y no más, y no es posible asignarle otras especies ni diferencias. Y dicha unidad es el supremo epíteto de Dios mismo, según toda la escuela teológica y también filosófica. La segunda correspondencia es la de la Santa Trinidad, es decir, que, así como in divinis hay una misma sustancia entre tres personas –Padre, Hijo y Espíritu Santo–, de igual modo una misma proporción se encontrará siempre entre tres términos, y nunca de más o de menos, como se dirá. La tercera correspondencia es que, así como Dios no se puede propiamente definir ni puede darse a entender a nosotros mediante palabras, nuestra proporción no puede nunca determinarse con un número inteligible ni expresarse mediante cantidad racional alguna, sino que siempre es oculta y secreta y es llamada irracional por los matemáticos. La cuarta correspondencia consiste en que, así como Dios nunca puede cambiar y está todo El en todo y todo en todas partes, de igual modo nuestra proporción es siempre, en toda cantidad continua y discreta, grande o pequeña, la misma y siempre invariable, y de ninguna manera puede cambiar ni de otro modo puede aprehenderla el intelecto, como nuestra explicación demostrará. La quinta correspondencia puede añadirse no sin razón a las cuatro anteriormente citadas: así como Dios confiere el Ser a la virtud celeste, por otro nombre llamada quinta esencia, y mediante ella a los otros cuerpos simples –es decir, a los cuatro elementos, tierra, agua, aire y fuego–, y a través de éstos da el ser a cada una de las otras cosas de la naturaleza, de igual modo nuestra santa proporción confiere el ser formal, según el antiguo Platón en su Timeo, al cielo mismo, atribuyéndole la figura del cuerpo llamado dodecaedro o, dicho de otro modo, cuerpo de doce pentágonos, el cual, como más abajo se demostrará, no puede formarse sin nuestra proporción. Y, del mismo modo, asigna una forma propia, diferenciada, a cada uno de los elementos, y así al fuego la figura piramidal llamada tetraedro, a la tierra la figura cúbica llamada hexaedro, al aire la figura llamada octaedro y al agua la conocida como icosaedro. Y según los sabios todos los cuerpos regulares están ocupados por dichas formas y figuras, como separadamente se dirá más abajo acerca de cada uno de ellos. Mediante éstos, nuestra proporción da forma a otros infinitos cuerpos llamados dependientes. Y no es posible proporcionar entre sí estos cinco cuerpos regulares ni se entiende que puedan circunscribirse a la esfera sin nuestra mencionada proporción, todo lo cual se pondrá de manifiesto más abajo.
Después de explicar la construcción de la serie de los cinco cuerpos regulares, Pacioli nos habla de la proporción de dichos cuerpos entre sí de este modo: Habiendo entendido cómo son suficientes estos cinco cuerpos regulares y habiéndose demostrado la imposibilidad de que sean más de cinco y el modo de sus dependientes de multiplicarse hasta el infinito, corresponde ahora establecer sus recíprocas proporciones en cuanto a capacidad y cabida y en cuanto su superficie, así como, antes de su área corporal, las inclusiones de unos en otros. Las proporciones de uno y otro serán siempre irracionales, debido a nuestra mencionada proporción, que interviene en su composición y formación, como se ha dicho, con excepción del tetraedro, del cubo y del octaedro; por la exactitud de las proporciones de éstos con respecto al diámetro de la esfera en la que se inscriben, podrá algunas veces ser racional, pero la del icosaedro y la del dodecaedro, comparadas con cualesquiera otras, nunca podrán ser racionales por la mencionada razón. No siempre es fácil seguir las explicaciones del autor por su lenguaje, aunque los términos apenas han cambiado en la actualidad; pero desde luego el llevar las operaciones a cabo en la práctica es imprescindible por lo que se pone al lector inmediatamente al trabajo, con regla y compás en la mano, concentrado, interesado en la construcción pues el libro entero es un desafío matemático para todos aquellos que han estudiado esa ciencia. Y aunque los medios de demostración de la proporción sean muchos y aun se apliquen de modo diferente, la clara exposición del florentino, como la de su maestro Euclides al que cita constantemente, son perfectamente válidas, insustituibles, para el día de hoy. Y aún en el mundo profano, o sea, sin destacar el discurso esotérico y la divinidad atribuida a los números y la matemática en general –y en particular a la proporción áurea. Efectivamente, constituyen desarrollos inspirados para entrenar y agilizar la inteligencia, para despertarla y relacionarla con la cosmogonía, la teúrgia y la deidad, asunto del que estamos tan necesitados. Esto, a cualquier nivel en que se las practique. A la esfera se la construye y define de modo desacostumbrado: Esfera es el cuerpo contenido por la huella del arco de circunferencia correspondiente a la mitad de un círculo siempre que, en cualquier forma que se tome el semicírculo y manteniendo firme la línea del diámetro, se haga girar alrededor de dicho arco hasta que retorne al lugar donde comenzó a moverse. O sea, trazado el semicírculo sobre una línea cualquiera, teniendo firme ésta, llévese dicho semicírculo con toda su revolución y el cuerpo así descrito se llamará esfera. Su centro será el del semicírculo que se ha hecho girar. En el tratado se destacan el número tres, necesario para cualquier proporción y el cinco, imprescindible y perfecto en la construcción del dodecaedro –figura de doce pentágonos de base y último sólido regular– al que designa como "nobilísimo". El tres significa los tres principios sagrados que dan lugar a cualquier manifestación por medio del cuaternario. Aritméticamente es aquel conformado por sus dos antecesores (1+2=3) y por ello el primer número triangular, geométricamente es el triángulo el que divide a la esfera en indefinidos fragmentos, es la suma o sea el acoplamiento, de lo activo, lo pasivo y lo neutro, conjunción que ilumina la conciencia. El triángulo tiene 3 lados, 3 vértices, tres ángulos y 3 bisectrices. Es el primer polígono perfecto y a la vez el 3 el primer número impar. Los tres primeros números son la base de la matemática, y su relación un símbolo de cualquier asociación o proporción, un caso particular de la cual es la sección áurea. En realidad la matemática es el desarrollo de estos tres primeros números y su sucesión indefinida; pero en ella tienen especial cabida los cinco sólidos regulares como representantes de los cuatro elementos creacionales y su centro, constituyendo un quinteto al que se le atribuye igualmente pertenecer al microcosmos, es decir, al hombre, como medida de todas las cosas, centro y receptáculo de la Creación universal, como puede verse en el célebre dibujo de Leonardo, conformando con su cuerpo extendido en un círculo la imagen del hombre en el mundo, y también la del microcosmos en el macrocosmos. El pentágono –o el pentalfa o estrella pitagórica y la estrella flamígera característica de la Masonería– es imprescindible en la construcción del dodecaedro, con el que se completa la imagen de la totalidad. Igualmente es el resultado de la suma o "matrimonio" entre el primer par y el primer impar (2+3=5), y llamado por ello número "nupcial". Dividir una recta finita dada en extrema y media razón llamaba Euclides a la "divina proporción" de Pacioli y lo muestra dividiendo precisamente un segmento en media y extrema razón, aunque luego lo hace formando tres cuadrángulos. En aras de presentarlo lo más sencillamente posible,7 veamos un segmento dividido en dos partes desiguales:
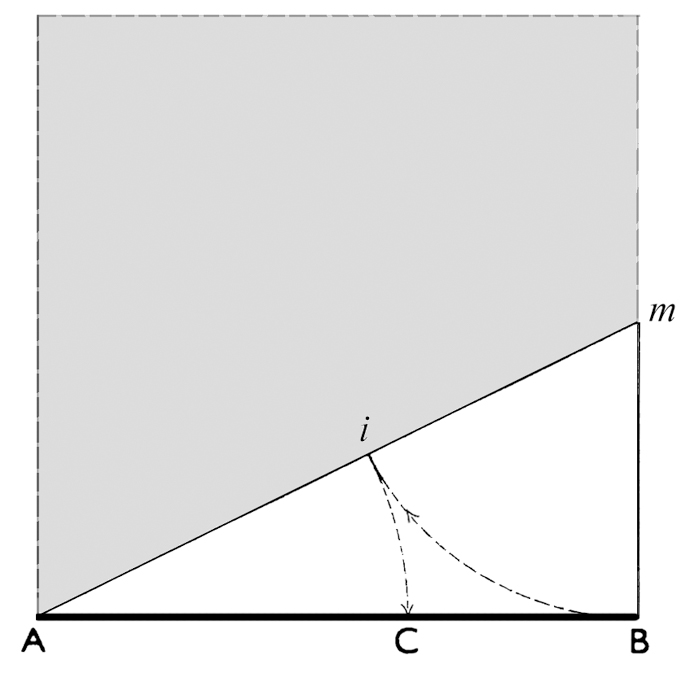
Donde la suprema ley de la proporción podría enunciarse como: se dice que una recta está dividida en media y extrema razón, cuando su longitud total es al segmento mayor como el segmento mayor es al menor. En nuestro caso AB es a AC como AC es a CB. Para obtener el punto de la media razón, en este ejemplo el punto C del segmento AB, se procede así (ver siguiente grabado): 1) Desde un punto m, que dista verticalmente de B la mitad de la longitud del segmento AB, se traza una recta hasta A. 2) Con el centro en m se traza el arco desde B que intersecta en i a la hipotenusa del triángulo rectángulo así formado. 3) Con el centro en A se traza desde i el arco que intersecta a su vez al segmento original marcando el punto C. De ese modo se encuentra determinada la división del segmento.
En cuanto a la expresión algebraica de esta definición, Matila Ghyka8 la escribe de esta manera: Consideremos… la igualdad a/b = a+b/a y, dividiendo por b los dos términos del segundo miembro (lo que no altera su valor), pongamos a/b = x, de donde:
o sea:
ecuación de segundo grado en x, cuyas raíces son:
es decir:
La raíz negativa, cuyo valor absoluto es igual al inverso de la raíz positiva porque x1 X x2 = –1 , corresponde a una posición de C exterior al segmento AB, y como no nos interesa por el momento, tomamos como valor de la razón buscada
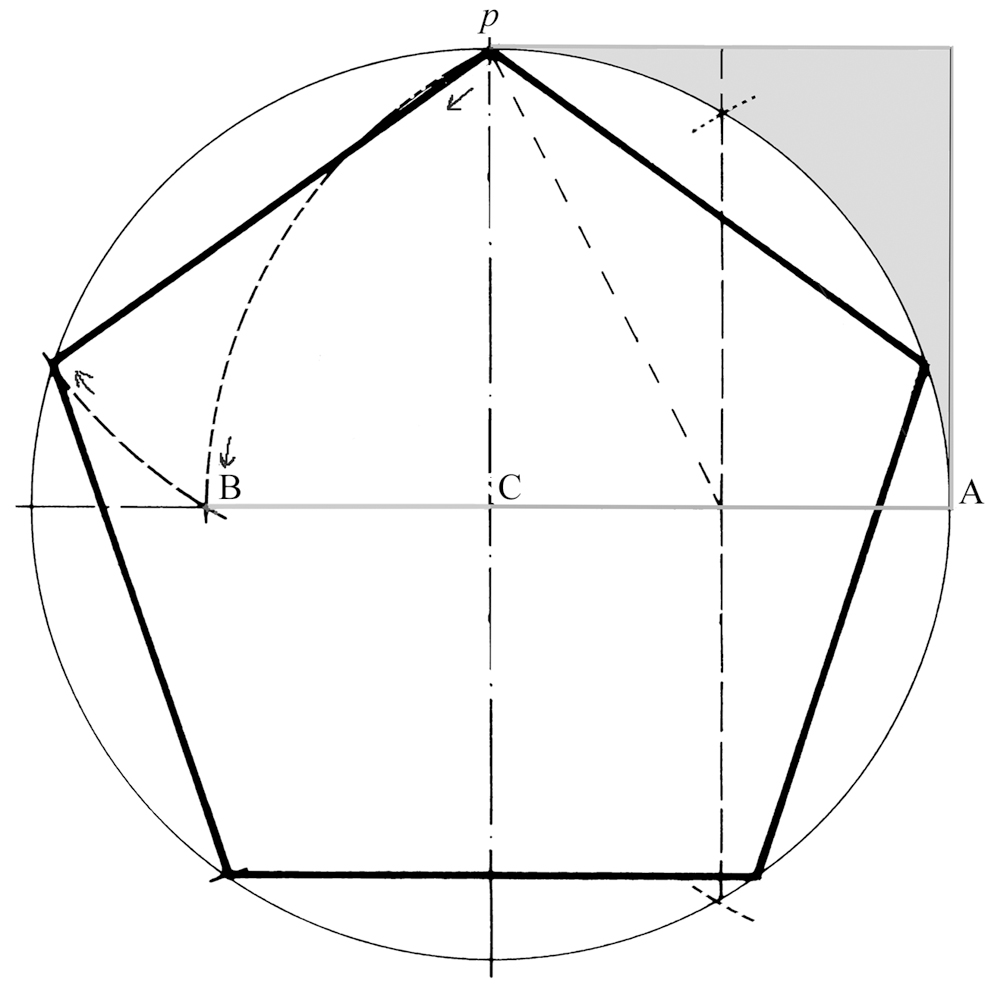
que es un número algebraico inconmensurable, trivial a primera vista… pero que posee características casi únicas entre todos los números de esta clase. Y afirma Ghyka en la misma obra: Se obtiene así la proporción que Pacioli llamaba proportion divina; Kepler que es el primero que menciona su interés en Botánica y para el cual "es una joya preciosa: uno de los dos tesoros de la Geometría"9 la llama también sección divina; Leonardo da Vinci le da el nombre de sección áurea, y de aquí la denominación de sección dorada (golden section, goldener Schnitt, section dorée), y la de número de oro… Su papel en la construcción del pentágono regular es imprescindible según afirma nuestro autor, lo que puede verse en el siguiente diagrama: A partir de un círculo y la cruz formada por dos de sus diámetros inscrita en él y habiendo obtenido el punto medio del radio CA, se traza desde dicho punto el arco desde p hasta su intersección con el mismo diámetro en B, lo que produce la determinación del segmento BA, el cual junto con su división en C constituye la proporción áurea. Con centro en p se traza un arco desde B que intersecta a la circunferencia y determina así el lado del pentágono regular inserto en ella.
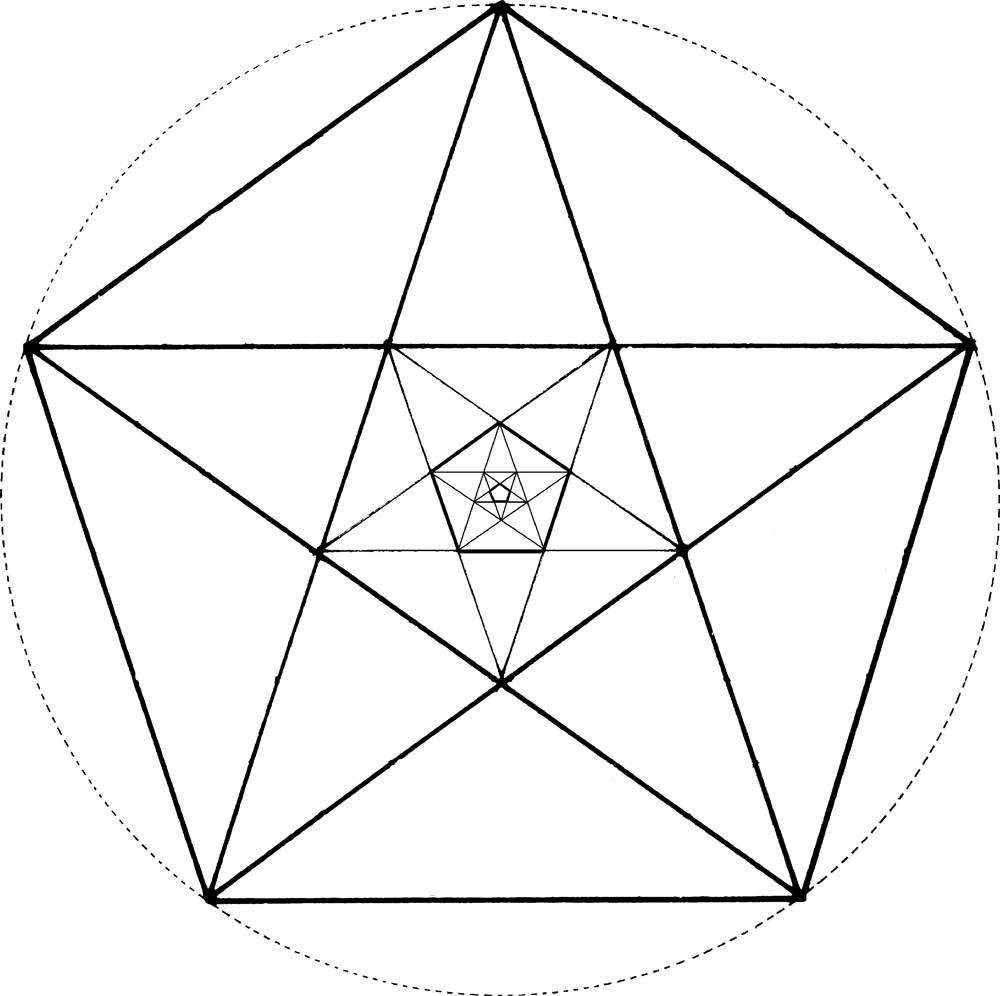
Como se sabe, la unión de sus vértices discontinuos produce la estrella o pentalfa, que a su vez contiene otro pentágono en el que hay otra estrella en cuyo centro se halla definido otro pentágono, etc. En el siglo XIX y el XX se han desarrollado los estudios sobre la proporción áurea, los que inclusive han investigado su presencia no sólo en la obra de arte sino en la propia estructura universal –tal cual fue sugerido por Pacioli– reconociéndola en la botánica, la mineralogía, etc. aunque tomando a esta extraordinaria proporción como la única posible, de modo literal, desvirtuando así el pensamiento del florentino que siempre puso el énfasis en la matemática en general como vehículo de conocimiento y teúrgia y no se circunscribió sólo a ese ejemplo de proporción10 que es un invariable algebraico sin solución regular, un irracional, por lo tanto inconmensurable, que progrede geométrica y orgánicamente y permanece implícito, como ya hemos dicho, en la construcción del pentágono. Por otra parte el fraile franciscano explica en su libro de diversos modos lo extraordinaria, matemáticamente, que es la "divina proporción".
A muchos de los que estudiaron en el bachillerato el teorema de media y extrema razón les resulta curioso que diversos autores le hayan dedicado obras, cuyas conclusiones al fin y al cabo son pobres respecto a la construcción de las formas de L. Pacioli en su apasionante aventura de la demostración de los cinco poliedros regulares y de sus dependientes.11 Se trata de una vía de conocimiento, en suma, que pretende lo invisible por medio de lo visible, una ley exotérica que manifiesta un esoterismo latente que la matemática como Ciencia Sagrada, expresa a su modo, por otra parte irrebatible, y que conforma un camino, o un auxilio, cuando es bien comprendido, análogo al de las otras utopías renacentistas con las que se complementa de manera natural. |
próximamente: XI. Otras utopías renacentistas: Atalanta Fugiens de Michael Maier: Alquimia, música, imagen |
| NOTAS | |
| 1 | Ed. Losada, Buenos Aires 1962. |
| 2 | Paul Vulliaud, La pensée ésotérique de Léonard de Vinci. Grasset, Paris 1910. |
| 3 | El libro de los Números Cuadrados. Eudeba, Buenos Aires 1973. |
| 4 | En este sentido se dice que Jacopo de Barbari (pintor), íntimo amigo de Pacioli, lo reúne con Durero que había viajado en 1506 a Bolonia para ser "iniciado en el arte secreto de la perspectiva". Recordemos que Piero della Francesca había publicado alrededor de 1492 De Prospectiva Pingendi. |
| 5 | Lo que no deja de ser una paradoja, casi un milagro, cuando se piensa que ello se lleva a cabo pese a la inestabilidad y brutalidad de las cortes de la época, signada por los condottieri, la traición, la hipocresía, el cinismo y la violencia. Debemos destacar igualmente la completa antítesis entre las utopías renacentistas que estamos estudiando respecto al Príncipe de Maquiavelo como expresión de la política "real". |
| 6 | Luca Pacioli, La Divina proporción. Ed. Akal, Madrid 1991. Introducción de Antonio M. González. Traducción de Juan Calatrava. Con algunos errores en el texto, probablemente a causa de la transcripción al castellano. Hay también una edición en castellano anterior. Losada, Buenos Aires 1959. |
| 7 | Los más interesados en el código de las matemáticas podrán acudir directamente a Euclides y al "inventor" de la "divina proporción", proporción áurea o número de oro, –distintas denominaciones que ha ido tomando esta relación entre tres términos que matemáticamente se escribe simplificando 1,618… y a la que se le ha otorgado como nomenclatura la letra griega Φ (Phi). |
| 8 | Estética de las proporciones en la naturaleza y en las artes, Ed. Poseidón, Hospitalet de Llobregat (Barcelona) 1983. Hay otras formas de hacerlo. También que hay otras proporciones áureas, análogas aunque menos perfectas. |
| 9 | "Mysterium Cosmographicum de admirabili proportione orbium caelestium, 1596. El otro tesoro es el teorema de Pitágoras." (Ibid.) |
| 10 | Los estudiosos actuales no sólo se han detenido en Pacioli y aún más lejos en Euclides, sino que han tratado de encontrarla enunciada en los clásicos, comenzando por el Timeo, y en cuanta construcción egipcia o griega ha pasado por sus manos, comenzando por el Partenón. El problema con ello es que se toma a la divina proporción como algo en sí y no justamente como una "proporción", es decir como una relación entre tres términos que es precisamente lo que la caracteriza. Especialmente cuando se la pone junto al triángulo 3-4-5, es decir el triángulo rectángulo pitagórico. Ambos teoremas (en el sentido etimológico del término) son para Kepler como hemos visto las bases de las matemáticas. |
| 11 | Estos dependientes, al decir del autor son "aquellos modos que poseen [los primeros] de multiplicarse infinitamente". Entre ellos trata de poliedros irregulares, la columna, la pirámide, etc. Es interesante destacar que en su obra De viribus quantitatis curiosamente no publicada aún, menciona a los conocidos "cuadrados mágicos" venidos supuestamente de la India a través de Bizancio. |
|
Indice |
Home page |